Debido a la crisis climática a nivel global, es importante considerar las emisiones atmosféricas por dióxido de carbono (CO2) que se generan a través del proceso de combustión de los combustibles fósiles, en la mayoría de los casos. Esto es con atención al Intergovernmental Panel Of Climate Change (IPCC), el cual, ha indicado que a partir del 2030, la atmósfera presentara cambios significativos debido al nivel de CO2, y en particular habrá resiliencia y adaptación por la crisis climática, asumiendo que arriba del 1.5 ºC podría haber eventos significativos en el cambio de diferentes compartimientos ambientales.
El principal objetivo del IPCC es reducir al máximo las emisiones de CO2, en particular, del sector industrial; es decir, de centrales eléctricas a base de combustóleo o carbón mineral, refinería del petróleo, sistemas portuarios, etc. La implementación de estrategias para la reducción y mitigación de emisiones incluye la descarbonización integrando la captura de CO2, su almacenamiento, y disposición final, ya sea en suelo o en mar.
Por lo anterior, es interesante conocer el sistema de carbonatos que se presenta en la atmósfera a partir de la concentración de CO2 y como contribuye al nivel de pH en la lluvia, debido a que a través del análisis por cromatografía, el ion hidronio y ion bicarbonato indican el pH de una muestra de lluvia.
$$CO_2 + H_2O \implies H_2CO_3;k_1=\frac{[H_2CO_3]}{[CO_2][H_2O]} = 1.3*10^{-3} … Eq(1)$$
$$H_2CO_3 \implies H^+ + HCO^-_3;k_2=\frac{[H^+][HCO^-_3]}{H_2CO_3} = 4.45*10^{-7} … Eq(2)$$
$$HCO^-_3 \implies H^+ + CO^{2-}_3;k_3=\frac{[H^+][CO^{2-}_3]}{HCO^-_3} = 2*10^{-11} … Eq(3)$$
Recordando que para determinar el pH de una muestra (por ejemplo de lluvia), el ion hidronio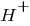 
, indica el nivel pH, de acuerdo con $$pH=-log[H^+]$$
Entonces, la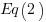 
resulta ser significativa debido a que su orden de reacción es menor que la 
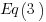; es decir, la 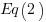es más frecuente que se lleve a cabo en la atmósfera
| Reacción | $$H_2CO_3 \implies$$ | $$H^+$$ | $$HCO^-_3$$ |
| Inicio | $$C_0$$ | $$—$$ | $$—$$ |
| Equilibrio | $$C_0-\alpha$$ | $$\alpha$$ | $$\alpha$$ |
Por lo que:
$$k_2=\frac{[H^+][HCO^-_3]}{H_2CO_3} = \frac{[\alpha][\alpha]}{[C_0-\alpha]} = 4.45*10^{-7}$$
Resolviendo y obtenido la ecuación cuadrática:
$$\alpha^2+4.45*10^{-7}\alpha-4.45*10^{-7}C_0=0$$
Equivalente a:
$$[H^+]^2+4.45*10^{-7}[H^+]-4.45*10^{-7}C_0=0$$
¿Cuál es el pH de una muestra de lluvia considerando una concentración de CO2 de 360 ppm?
